탐색
: 저장된 정보들 중에서 원하는 값을 찾는 것
예) 리스트에 숫자들이 뒤죽박죽 나열되어 있는데 그 중 '5' 라는 숫자가 어디에 있는지 찾는 것
탐색의 2가지 방법
: 선형탐색(Linear Search), 이진탐색(Binary Search)
선형 탐색 알고리즘 (linear search algorithm)
리스트의 처음부터 끝까지 순서대로 하나씩 탐색을 진행하는 알고리즘
이진 탐색 알고리즘 (binary search algorithm)
정렬된 리스트에서 중간값이랑 비교해보고 반씩 제외하면서 찾는 것
<파이썬으로 알고리즘 작성해보기>
1. '선형 탐색(Linear Search)' 알고리즘을 사용해서 어떤 원소가 리스트 안에 포함되어 있는지 확인하기
* for 문 사용
def linear_search(target,some_list):
for i in range(len(some_list)):
if target == some_list[i]:
return i
return None
#테스트
print(linear_search(1,[3,4,1,9]))
print(linear_search(9,[3,4,1,9]))
print(linear_search(100,[3,4,1,9]))
실행결과 >

* while 문 사용
def linear_search1(target,some_list):
i = 0
while i < len(some_list):
if target == some_list[i]:
return i
i += 1
return None
#테스트
print(linear_search1(1,[3,4,1,9]))
print(linear_search1(9,[3,4,1,9]))
print(linear_search1(100,[3,4,1,9]))
실행결과 >

2. '이진탐색(Binary Search)' 알고리즘을 사용해서 어떤 원소가 리스트 안에 포함되어 있는지 확인하기
이진 탐색 알고리즘은 선형 탐색 알고리즘과 달리, 정렬된 리스트를 전제로 한다.
정렬된 리스트가 아니면 이 알고리즘은 적용이 불가능하다.
이진탐색에선 비교를 1번씩 거칠 때마다 탐색 범위가 (대략) 절반으로 줄어든다.
로직 설명 :
1. 리스트의 첫 번째 인덱스 (0) 와 마지막 인덱스 (리스트 길이 - 1 ) 를 합하여 2로 나눈 후, 중간 인덱스로 지정한다.
나눌땐 나머지 버림, 몫만 챙김 ex) 5/2 의 몫은 2
2. 찾을 값이(target), 중간 인덱스 값 보다 작은 경우 중간 인덱스 포함 그 이후 인덱스 값들은 검색 범위에서 제외한다.
중간 인덱스 - 1 을 마지막 인덱스로 삼고 다시 비교한다.
3. 찾을 값이(target), 중간 인덱스 값 보다 큰 경우 중간 인덱스 포함 이전 인덱스 값들은 범위에서 제외한다.
중간 인덱스 + 1 을 첫번째 인덱스로 삼고 다시 비교한다.
4. 찾을 값이(target) 중간 인덱스의 값과 같으면 인덱스를 return 한다.
def binary_search(target, some_list):
first_index = 0
last_index = len(some_list) - 1
while first_index <= last_index:
mid_index = (first_index + last_index) // 2
if some_list[mid_index] == target:
return mid_index
elif some_list[mid_index] < target:
first_index = mid_index + 1
else:
last_index = mid_index -1
return None
print(binary_search(2, [2, 3, 5, 7, 11]))
print(binary_search(0, [2, 3, 5, 7, 11]))
print(binary_search(5, [2, 3, 5, 7, 11]))
print(binary_search(3, [2, 3, 5, 7, 11]))
print(binary_search(11, [2, 3, 5, 7, 11]))
실행결과 >
<탐색 알고리즘 평가 Big O>
점근 표기법 Big-O Notation
시간 복잡도
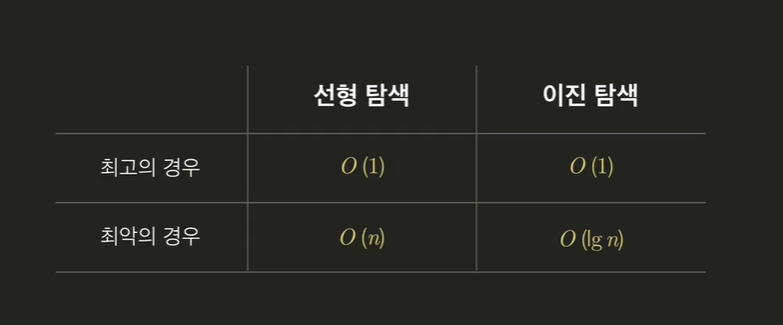
알고리즘 평가는 최악의 경우 (제일 긴 시간이 드는 경우) 로 따지는데
선형 탐색은 O(n) ( 읽는 법 -> Big O of n -> 빅 오 오브 엔 )
이진 탐색은 O(lg n) ( 읽는 법 -> Big O of lg n -> 빅 오 오브 로그 엔 )
선형 탐색을 하려면 최악의 경우에 n개를 봐야하니까 O(n)
이진 탐색을 하려면 최악의 경우에

개를 봐야하니까 lg n 즉 O (lg n)
'IT > Python' 카테고리의 다른 글
| 구글 코랩 한글 폰트 설치 코드 (1) | 2025.07.04 |
|---|---|
| 회귀분석 예시 - 광고 지출이 오가닉 유입에 영향을 미칠까? (코드와 해석 포함) (0) | 2024.03.21 |
| [Python] 팰린드롬 palindrome 거꾸로 해도 같은 단어인지인지 확인하기 (0) | 2022.01.21 |
| [Python] 데이터 시각화 Seaborn 라이브러리 (Jupyter Notebook) (0) | 2022.01.20 |
| [Python] 상관관계 시각화 히트맵, 클러스터 (ft. Jupyter Notebook) (0) | 2022.01.20 |




댓글