회귀분석
광고 지출이 오가닉 유입에 영향을 미치는지 실행해보겠습니다
1. 회귀분석 코드
2. 회귀분석 결과 해석
3. 회귀분석 시각화
회귀분석 코드
아래 코드를 구글 코랩이나 파이썬 환경에서 실행하면
광고비지출(ads_cost)이 오가닉 유입 방문자수(organic_users)에 미치는 영향을 분석할 수 있습니다.
import pandas as pd
import numpy as np
import statsmodels.api as sm
# 데이터셋 생성
data = {
'date': [20230101, 20230102, 20230103, 20230104, 20230105, 20230106, 20230107, 20230108, 20230109, 20230110,
20230111, 20230112, 20230113, 20230114, 20230115, 20230116, 20230117, 20230118, 20230119, 20230120,
20230121, 20230122, 20230123, 20230124, 20230125, 20230126, 20230127, 20230128],
'organic_users': [3322, 4521, 4733, 4555, 4613, 4452, 4008, 4301, 4612, 4473,
4101, 4175, 3957, 3828, 4149, 4506, 4289, 4329, 4197, 3960,
3584, 3938, 4184, 4018, 4237, 4260, 4104, 3915],
'ads_cost': [241796, 345260, 307354, 246686, 310523, 381765, 422571, 475126, 434647, 431534,
429073, 432798, 434022, 424597, 412765, 415542, 420396, 423867, 419263, 372842,
386598, 432082, 430844, 430031, 413923, 392118, 356049, 437503]
}
# 데이터프레임 생성
df = pd.DataFrame(data)
# 회귀 분석을 위한 모델 설정
X = df[['ads_cost']] # 독립 변수
y = df['organic_users'] # 종속 변수
X = sm.add_constant(X) # 상수항 추가
# 회귀 모델 적합
model = sm.OLS(y, X).fit()
# 회귀 결과 출력
print(model.summary())
이렇게 실행해 보면
회귀 결과 출력이 아래와 같이 나옵니다
OLS Regression Results
==============================================================================
Dep. Variable: organic_users R-squared: 0.064
Model: OLS Adj. R-squared: 0.062
Method: Least Squares F-statistic: 28.21
Date: Thu, 21 Mar 2024 Prob (F-statistic): 1.78e-07
Time: 06:52:52 Log-Likelihood: -3118.8
No. Observations: 416 AIC: 6242.
Df Residuals: 414 BIC: 6250.
Df Model: 1
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const 4545.1166 41.793 108.754 0.000 4462.964 4627.269
ads_cost -0.0005 9.51e-05 -5.312 0.000 -0.001 -0.000
==============================================================================
Omnibus: 1.061 Durbin-Watson: 0.505
Prob(Omnibus): 0.588 Jarque-Bera (JB): 1.060
Skew: -0.122 Prob(JB): 0.589
Kurtosis: 2.960 Cond. No. 8.57e+05
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The condition number is large, 8.57e+05. This might indicate that there are
strong multicollinearity or other numerical problems.
회귀 분석 결과 해석
위 결과를 해석해 보겠습니다
R-squared (결정 계수): 0.064로, 종속 변수의 변동량 중 독립 변수로 설명할 수 있는 비율을 나타냅니다. 이 모델은 종속 변수의 변동 중 약 6.4%를 설명할 수 있습니다.
Adj. R-squared (조정된 결정 계수): 0.062로, 독립 변수의 수와 샘플 크기를 고려하여 보정된 결정 계수입니다.
F-statistic: 28.21이며, 회귀 모델의 적합도를 검정하는데 사용됩니다. 이 값이 클수록 회귀 모델이 데이터에 잘 적합되었다고 볼 수 있습니다.
Prob (F-statistic): 1.78e-07로, F-통계량의 p-value입니다. 이 값이 매우 작으므로 회귀 모델은 통계적으로 유의미합니다.
coef (계수): ads_cost의 계수는 -0.0005입니다. 이는 ads_cost가 1 증가할 때 organic_users가 평균적으로 0.0005만큼 감소한다는 것을 의미합니다.
P>|t| (p-value): 0.05보다 작으므로 ads_cost의 계수는 통계적으로 유의미합니다.
const (상수항): 4545.1166으로, ads_cost가 0일 때 organic_users의 평균값입니다.
이 결과를 종합해보면,
✔ ads_cost가 organic_users에 미치는 영향은 통계적으로 유의미하지만,
✔ 결정 계수가 매우 낮으므로 ads_cost가 organic_users를 설명하는 데 큰 영향을 미치지 않는다고 할 수 있습니다.
회귀분석 시각화
회귀분석 결과를 시각화하기 위해서는 '회귀선'과 '데이터 포인트'를 함께 그려보면 좋습니다.
아래는 회귀선과 데이터 포인트를 함께 시각화 해주는 코드입니다.
# 회귀선 그리기
plt.figure(figsize=(10, 6))
plt.scatter(df['ads_cost'], df['organic_users'], color='blue', label='Data Points')
plt.plot(df['ads_cost'], model.predict(X), color='red', label='Regression Line')
plt.title('Regression Analysis')
plt.xlabel('Ads Cost')
plt.ylabel('Organic Users')
plt.legend()
plt.grid(True)
plt.show()
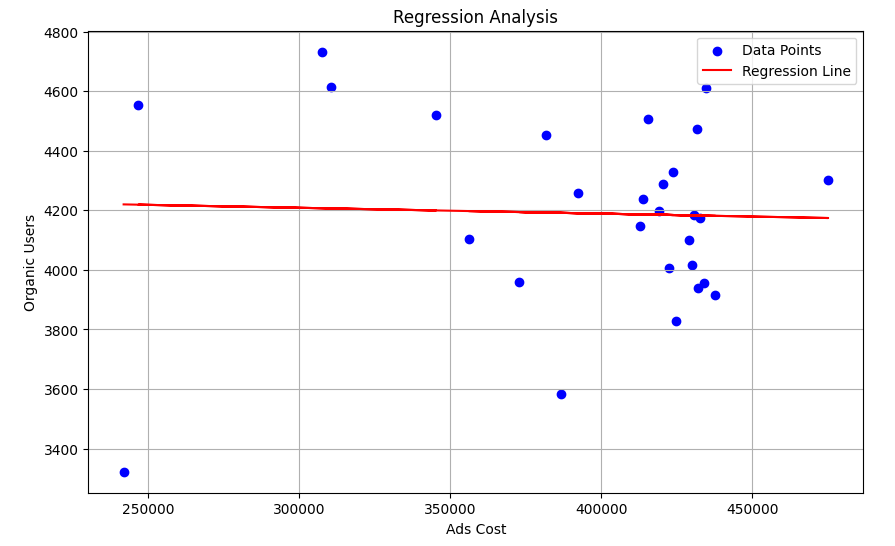
data point 와 regression line 이 의미하는 것?
"data point"는 데이터 집합에서 관찰된 개별 데이터를 나타냅니다. 각각의 데이터 포인트는 독립 변수(여기서는 광고비)와 종속 변수(여기서는 오가닉 유입 방문자수)의 값을 가지고 있습니다. 데이터 포인트는 산점도(Scatter plot)에서 점으로 나타납니다.
"Regression line"은 회귀 분석에서 추정된 선형 회귀 모델의 결과물입니다. 이는 독립 변수와 종속 변수 간의 관계를 나타내는 직선입니다. 회귀 분석은 이러한 회귀선을 찾는 과정입니다. 회귀선은 일반적으로 최소제곱법(Least Squares)을 사용하여 데이터 포인트와의 오차를 최소화하도록 결정됩니다.
따라서 산점도에서 데이터 포인트와 함께 그려진 회귀선은 데이터의 분포를 시각적으로 나타내며, 독립 변수와 종속 변수 간의 관계를 보여줍니다. 회귀선은 주어진 독립 변수 값에 따라 종속 변수의 예측값을 제공하며, 이를 통해 두 변수 간의 관계를 이해하고 예측할 수 있습니다.
'IT > Python' 카테고리의 다른 글
| 구글 코랩 한글 폰트 설치 코드 (1) | 2025.07.04 |
|---|---|
| [알고리즘] 선형탐색 , 이진탐색 (feat. 파이썬, 시간복잡도) (0) | 2022.02.18 |
| [Python] 팰린드롬 palindrome 거꾸로 해도 같은 단어인지인지 확인하기 (0) | 2022.01.21 |
| [Python] 데이터 시각화 Seaborn 라이브러리 (Jupyter Notebook) (0) | 2022.01.20 |
| [Python] 상관관계 시각화 히트맵, 클러스터 (ft. Jupyter Notebook) (0) | 2022.01.20 |




댓글